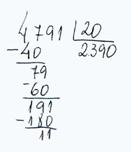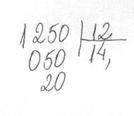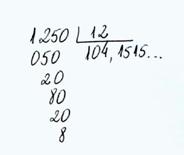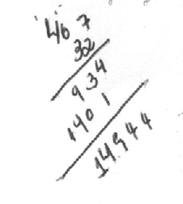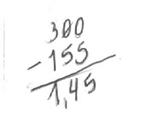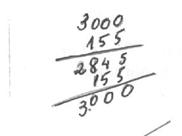|
Seja Bem-vindo Cristiane Rodrigues Reina Soriani - Home Page |
|
|
|
CRISTIANE RODRIGUES REINA SORIANI
UMA PROVA DE MATEMÁTICA ...
O PROFESSOR DAS SÉRIES INICIAIS DO ENSINO FUNDAMENTAL...
Monografia apresentada como exigência final para conclusão do Curso de Especialização em Educação Matemática da Universidade Estadual de Londrina. Orientadora: Profa. Dra. Regina Luzia Corio de Buriasco
- Londrina - 2000
Dedico este trabalho à minha irmã, Joselen, que está iniciando este ano a sua carreira no magistério e aos meus sobrinhos Bruna e Vinícius, que eles cresçam, estudem, vençam e brilhem.
AgradecimentosEm primeiro lugar quero agradecer a Deus, pois Ele é a fonte de toda e verdadeira sabedoria.A realização deste trabalho se deve muito a atenção e a dedicação da minha orientadora Profª. Drª. Regina Luzia Corio de Buriasco, sobretudo por sua disponibilidade e paciência como também das Profªs. Ms. Luciana Gastaldi S. Souza, Márcia Cristina de Costa Trindade Cyrino e Denise Trindade Moreira pelo incentivo e apoio dispensados em todos os momentos deste curso.Minha gratidão também aos professores que gentilmente se dispuseram a participar deste trabalho, tornando-o possível.Agradeço às minhas colegas da Escola Municipal “Prof. Dr. Carlos da Costa Branco”, em especial às Profªs. Arlete Maria Lopes Ribeiro, Cacilda Ferraro e Eda Ângelo que atuam no período matutino na escola, mas se dispuseram a me substituir à tarde sempre que foi preciso, à Dolores do Carmo Dias Marczuk e Rosiclér Rodini Mazironi, respectivamente diretora e surpevisora da escola, por terem dado o aval para a minha dispensa nas sextas-feiras sempre demonstrando muito interesse em colaborar.
Agradeço também à Profª. Helena Aida da Silva pelo esmero com que efetuou a revisão ortográfica e gramatical deste trabalho. Ao Algacir, meu esposo, um agradecimento especial e carinhoso, ele não mediu esforços para que eu saísse vitoriosa deste curso, me apoiando, ajudando e incentivando sempre com grande carinho e dedicação.
Sumário
Resumo ............................................................................................................... 006Introdução .......................................................................................................... 007Algumas considerações sobre Avaliação, Erro e Formação de Professores .... 010 Um Perfil dos Professores que fizeram parte do Trabalho ............................... 017 Uma Breve Descrição da Prova ......................................................................... 042 Analisando as Questões .................................................................................... 048 Algumas Sugestões .......................................................................................... 096 Considerações Finais ........................................................................................ 114 Referências Bibliográficas ................................................................................ 117 Anexos .............................................................................................................. 118
Resumo
Mediante a aplicação da prova de Matemática da 4ª. Série do Ensino Fundamental constante da Avaliação Estadual – PR/97 a cinqüenta professores de Pré a 4ª. Série atuantes na rede Municipal de Ensino de Londrina, apresento um levantamento e breve análise dos erros cometidos, bem como, uma sugestão de trabalho para os conteúdos nos quais a incidência de erro foi maior. A pretensão deste trabalho é oferecer ao professor das séries iniciais um texto que lhe permita uma reflexão sobre o quanto do conteúdo matemático ele não se apropriou e quanto isso pode influenciar na aprendizagem de seus alunos. Introdução
“O futuro pertence àqueles que confiam na beleza de seus sonhos”, não sei quem escreveu isto, mas achei que deveria passar para você[1], pois todos temos sonhos e devemos buscá-los sempre.
Estou na rede municipal de ensino de Londrina há 16 anos. E, como cresci nesse tempo todo! Cresci a ponto de perceber que nós não precisamos “parar” para sermos ultrapassados basta que nos acomodemos um pouco.
Em 1992, formei-me em Matemática, pela UEL e saiba, que esse curso foi um desafio, pois como a maioria das pessoas, eu não tive uma boa “Alfabetização Matemática”, isto é, fui decorando uma porção de regras, sem ao menos saber para que serviam. Isso me fez sentir um certo desconforto que não quero que meus alunos sintam.
Resolvi então, me aperfeiçoar um pouco mais. Daí a decisão em cursar, em 1999, a “Especialização em Educação Matemática” na UEL. O curso foi ministrado nas sextas-feiras o dia todo e nos sábados pela manhã, mas com alguns sábados inteiros também.
Tive então, de pedir dispensa na prefeitura para faltar às sextas-feiras, pois, nesta época eu estava lecionando o dia todo. Pela manhã Matemática em um colégio particular e a tarde, 2ª. Fase do “Ciclo Básico” pela prefeitura. Com o aval da diretora da escola municipal em que atuo, foi me concedida a dispensa.
Durante o ano do curso, tive o apoio e colaboração de todos os meus colegas da Escola Municipal “Prof. Dr. Carlos da Costa Branco” que não mediram esforços para suprirem minha ausência em todas as sextas-feiras do ano letivo, tendo que alterar até mesmo horários de reuniões e grupos de estudos.
Minha orientadora e eu discutimos e escolhemos o tema a ser desenvolvido nesta monografia. Decidimos que faríamos um trabalho voltado aos professores das séries iniciais, pois é aí que sinto estar a chave de uma mudança para melhoria do ensino de Matemática.
Resolvemos aplicar a um grupo de professores de Pré a 4ª. Série do Ensino Fundamental da Rede Municipal de ensino a prova de matemática da Avaliação Estadual – PR / 97, aplicada aos alunos de 4ª. Série.
O objetivo do nosso trabalho é analisar o que foi resolvido, como foi resolvido, enxergando o “erro” como gerador de progresso, levando sempre à reflexão. É a partir da análise dos “erros” que serão sugeridas atividades para que determinados conteúdos sejam melhor aproveitados.
Não estou escrevendo esta monografia para professores de matemática exclusivamente, é para você, professor das séries iniciais que como eu, quer que nossos alunos sejam melhores que nós, que enxerguem o lado social do conhecimento matemático, que dêem significado à Matemática em sua vida, que interpretem, criem maneiras de resolver seus problemas, raciocinem, critiquem, enfim, que exerçam sua cidadania.
Algumas considerações sobre Avaliação, Erro e Formação de professores
Para que possamos nos entender melhor, farei uma rápida explanação sobre como enxergo a “Avaliação”, o “Erro” e a “Formação de Professores” no processo ensino-aprendizagem.
1. Avaliação
A avaliação é um processo de sustentação da aprendizagem que, no meu entender, se inicia antes mesmo do planejamento escolar. Porque para que possamos fazer o planejamento já devemos ter “escolhido” dentre tantos conteúdos, quais trabalharemos e qual a prioridade de cada um. E, isto já é uma parte do processo de avaliação.
Uma das funções da avaliação é ajudar o aluno a aprender e o professor a ensinar, pois deve haver sempre uma reflexão a partir dela.
É comum confundir “avaliação” com “prova”, contudo esses dois termos não são sinônimos, a avaliação é um processo e a prova é um dos instrumentos de medida utilizado no processo de avaliação; é como se fosse uma ferramenta, mas existem outras,por exemplo a observação.
Temos de contar com uma “avaliação formativa” durante todo o processo. Mas, o que vem a ser “avaliação formativa”?
É aquela que tem como objetivo melhorar a formação do aluno, sua preocupação não é classificar, dar notas, punir ou recompensar, mas sim ajudar o aluno a aprender. “Uma avaliação que permita aos alunos identificar seus erros, acertos e lacunas; e ao mestre, destacar os ganhos as dificuldades de cada aluno para poder ajuda-los a progredir mais.” (André, 1999 , p. 22)
A avaliação deve ser assumida também como uma estratégia para a compreensão do estágio de aprendizagem em que o aluno se encontra, tendo em vista tomar decisões para que ele possa avançar no seu processo de aprendizagem, para que possa realizar-se como sujeito crítico dentro da sociedade em que vive.
Sempre temos de nos perguntar:
Avaliamos por quê? Para quê?
Devemos refletir sobre as respostas para essas perguntas, tendo sempre em vista uma avaliação diagnóstica.
Para o professor, a avaliação propicia, além de identificar as dificuldades dos alunos, melhorar seu nível de compreensão das formas de aprendizagem, auto-avaliar-se e avaliar o processo de ensino-aprendizagem. A avaliação deve ser sistemática, ou seja, organizada, planejada, executada, envolvendo todos os elementos do processo. Todos avaliam e todos são avaliados. Além disso, a avaliação deve, em muitos momentos, ser objeto ela mesma de uma avaliação.
Sendo assim, a “avaliação” permitirá reorganizar o processo de ensino-aprendizagem, gerar novos desafios, melhorar a aprendizagem e melhorar o ensino.
2. O Erro
O erro, no processo ensino-aprendizagem, vem sendo apontado como algo negativo, merecendo punição. Mas, não foi esta visão que norteou este trabalho.
Ao pedir que algumas colegas resolvessem a prova da 4ª. Série, deixei bem claro que analisaria cada questão com cuidado e que os erros, se é que existiriam, seriam usados para, a partir deles, dar as minhas sugestões de trabalho.
O erro gera progressos, pois leva à reflexão. Será que a lâmpada foi inventada na primeira tentativa? Claro que não! Houve “erros” e, quanto mais erros, mais perto da lâmpada estávamos.
O “erro” aponta o que não se sabe ainda por completo, e sendo assim, a partir dele podemos levantar hipóteses que nos levem ao caminho seguido pelo aluno para que cometesse o erro, com isso, poderemos escolher o percurso a ser seguido para completar o conhecimento em questão. Para isto, temos de aceitar o “erro” como normal, aprender a interpretá-lo, passando assim a usá-lo de forma mais produtiva e construtiva.
É assim que temos de “enxergar” os erros cometidos, eles deverão nortear nosso trabalho, nos ajudarão a conhecer melhor a cada aluno, tornando nosso trabalho mais fácil, pois teremos sempre algo que nos guiará.
Para que nosso trabalho docente flua melhor, é preciso que o aluno participe ativamente de todo o processo, é preciso que ele fale, que se exponha, para que possa também se corrigir. Vocês já repararam que quando falamos, ou explicamos algo a alguém, percebemos nossos erros? Com o aluno acontece o mesmo, ao ouvir-se ele pode perceber seu erro e sozinho corrigí-lo.
Você já tinha pensado assim!? Se não tinha, tente a partir de agora! Você verá como tudo ficará mais fácil.
“Errar” é natural no desenvolvimento do ser humano, então, cabe a nós, professores, usarmos esse “erro” em favor do processo ensino-aprendizagem.
3. A “Formação de Professores”
No curso de Especialização, tive um encontro de dois dias com a Prof. Dra. Ocsana Danyluk, que falou sobre “Alfabetização Matemática” e me fez enxergar uma realidade que ainda não tinha percebido.
Na Introdução desta monografia mencionei que, como a maioria das pessoas, eu não havia tido uma boa “alfabetização matemática” e vou tentar explicar agora o porquê.
Quando entramos na escola, nos é apresentada uma matemática de continhas e problemas, que muitas vezes nada tem a ver com nossa realidade. Sei que agora isso já melhorou muito, pois nos preocupamos em adequar os “problemas” à realidade de nossos alunos, mas na minha época isso não acontecia, se aconteceu com você, ótimo, foi um privilégio. A escola fazia questão também de quase deixar claro que a Matemática era uma disciplina difícil e que somente alguns, de inteligência privilegiada, poderiam dominá-la. Assim foi em todo o processo escolar que passei.
No magistério, a matemática foi pobre; alguns conteúdos nunca foram trabalhados, como por exemplo trigonometria ou mesmo logaritmo, se eu estiver falando “grego” pra você agora, é porque com você aconteceu o mesmo.
Mas, é esse curso que forma o professor das séries iniciais, é este professor que vai “ensinar” os primeiros passos sistemáticos da Matemática, esse professor que, muitas vezes, “não gosta” muito da matéria e que, se pudesse fugiria dela. De uma forma ou de outra, acabamos passando isso pro nosso aluno.
Não é culpa nossa, o que sentimos foi acontecendo sem que nos déssemos conta, eu mesma, nunca tinha parado pra pensar nisso.
Quando terminamos o Magistério, é hora de escolhermos nossa “faculdade” e o pensamento de muitos é “vou escolher um curso que não tenha Matemática” , ou que tenha pouca, então, a maioria escolhe Pedagogia, mesmo porque, é o curso que dá verdadeira continuidade à carreira, teoricamente falando e, neste curso, quem ministra a “Didática da Matemática” , como no magistério, não é alguém com formação específica em Matemática.
Mas, voltemo-nos então para alguns poucos que gostam da Matemática, que sempre tiveram facilidade com a disciplina e escolhem então o curso de “Matemática” para sua “faculdade”, nesse curso também, quem ministra as disciplinas específicas da licenciatura, como “Didática”, “Psicologia” e outras, não é alguém com formação específica em Matemática, já, os demais professores do curso com exceções, claro, só se importam com a Matemática em si, desvinculada do ensino, portanto na verdade, ninguém aprende a “ensinar Matemática”, talvez achem que não é preciso, mas nós que estamos na sala de aula, sabemos o quanto isto é importante.
Discutimos no encontro com a Profª. Drª. Ocsana Danyluk qual deveria ser a solução para isto e concluímos que a mudança deve iniciar em cada um de nós. Fazendo o pouco que pudermos para melhorar a situação.
Não pense você, que eu me coloco numa situação diferente da sua, admiti no início o quão desafiador foi o curso (Matemática) para mim. E, sabem onde verdadeiramente aprendi o que deveria saber para ensinar? Isto mesmo, dando aulas, eu tive de estudar muito pra poder ensinar meus alunos. Tenho certeza que com você também foi assim, é assim. Nós não podemos “parar”, não podemos repetir com nosso aluno o que fizeram conosco, ninguém tem culpa agora, mas todos temos de fazer algo para melhorar.
Vamos nos auto-avaliar sempre, admitir nossas falhas e buscar saná-las de alguma forma.
A “Rede Municipal de Ensino” oferece ótimos cursos em suas “Semanas Pedagógicas”, é um trabalho sério que é feito com cuidado e carinho, aliás merece ser elogiado e mais, merece que quando participarmos, o façamos com responsabilidade visando o melhor para nós como educadores e para os nossos alunos. Não devemos ir por obrigação e ficar lá só de corpo presente, devemos aproveitar, questionar, “sugar” mesmo os “docentes” eles estão lá pra isso e, com certeza é isso que querem de nós.
Um Perfil dos Professores que Fizeram parte do Trabalho
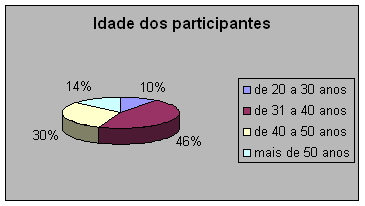
Para que o trabalho ganhasse um maior significado, os participantes responderam a um questionário para se ter uma idéia de quem eram esses professores. Os dados colhidos a partir dele estão nas tabelas e gráficos apresentados a seguir.
Os participantes deste trabalho atuam como professores da Rede Municipal de Ensino, de Pré a 4ª. Série do Ensino Fundamental do Município de Londrina, ao todo são cinqüenta professores.
O gráfico e a tabela nos mostram que a maioria dos professores participantes tem entre trinta e um e quarenta anos. Vejo esse dado como aspecto positivo, pois se espera que nesta faixa etária a pessoa já saiba o que quer e aja com responsabilidade. Por outro lado, muitas vezes, a idade cronológica não é relevante, pois sabemos que existem idosos que se sentem eternamente “jovens”, cheios de vida e também jovens que se dedicam com responsabilidade ao que fazem. Na verdade, o que importa mesmo é a motivação de cada um.
A tabela nos mostra que a maioria dos participantes (oitenta por cento) tem formação superior, dos quais vinte por cento têm pós-graduação. O curso escolhido pela maioria foi “Pedagogia” o que vem ao encontro com o que mencionei na “Formação de Professores”.
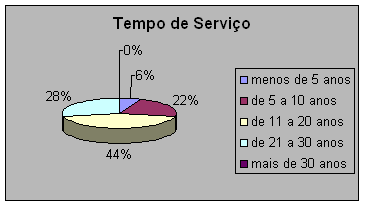
O gráfico e a tabela nos mostram que a maioria dos professores participantes está, teoricamente, no “auge” de sua carreira, entre onze e vinte anos de atuação no magistério. Penso que este tempo de atuação faz com que se tenha uma boa visão de “educação” e bastante experiência. Para mim, este é um dado positivo.
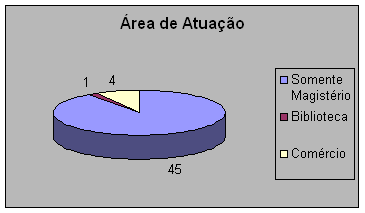
Que maravilha!!! A maioria absoluta dos professores participantes tem dedicação profissional exclusiva ao magistério.
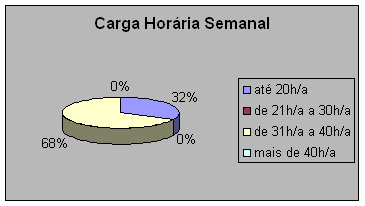
A tabela e o gráfico nos fazem ver que a grande maioria dos participantes trabalha o dia todo e, comparando com o gráfico anterior, notamos que atuam o dia todo no magistério. É sabido por todos nós que temos de buscar alternativas para melhorar nossos rendimentos, mas será que o fato da maioria estar todo tempo ligada ao magistério foi escolha de cada um? Ou será que foi uma imposição do mercado de trabalho e da sociedade? Esta é uma pergunta que eu deveria ter feito a eles.
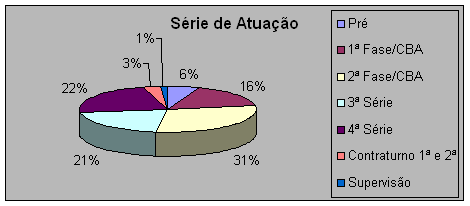
A maioria dos participantes atua na Segunda Série do Ensino Fundamental, isto nos mostram a tabela e o gráfico. Como já atuei em segundas séries, sei que é nesta fase que a maioria dos professores introduz, sistematicamente, a multiplicação e a divisão, conteúdos estes que apresentam dificuldades que se refletem ao longo do processo de aprendizagem da Matemática.
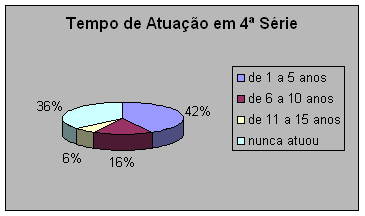
A tabela e o gráfico nos fazem ver que a maioria dos professores participantes já atuou em quartas séries do Ensino Fundamental, penso que isto seja bom, pois os professores já têm conhecimento dos conteúdos e “exigências” inerentes a esta série.
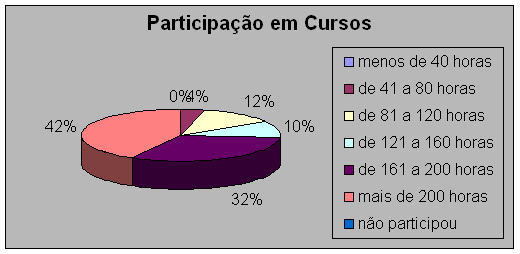
O perfil mostrado por este gráfico e esta tabela não me surpreendeu, pois a Secretária Municipal de Ensino promove periodicamente cursos aos professores, dentro de seu horário de trabalho. Temos “Práticas Pedagógicas”, “Grupo de Estudos” e a “Semana Pedagógica”, todos com certificados. Então, os professores que optaram por itens abaixo de 200 horas devem ser professores que iniciaram na rede há pouco tempo ou estiveram em “licença” prolongada.
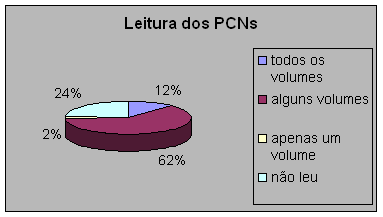
O gráfico e a tabela nos indicam que a maioria dos professores leu “alguns volumes” dos “Parâmetros Curriculares Nacionais”. Acredito que este resultado se deve ao fato de que no início do ano letivo de 1999 tivemos como tema das “Práticas Pedagógicas” os “PCNs”, portanto alguns volumes foram lidos quase que na íntegra, como o “Introdução” e o “Temas Transversais”. Mas os “PCNs” não foram “dados” aos professores, então o acesso a eles é mais difícil. Penso que cada professor deve ter seu próprio conjunto dos PCN.
A tabela nos mostra que a maioria dos professores utiliza livros didáticos, adotados ou não, e a “Proposta Curricular do Município de Londrina” para preparar suas aulas. Pouquíssimos utilizam os “PCNs”. A “Proposta Curricular” e os livros didáticos são de fácil acesso ao professor, cada um tem seu volume da “Proposta Curricular”, já os “PCNs”, não . O uso da “Proposta Curricular” é um dado positivo, pois comparada aos “PCNs”, não encontramos grandes diferenças. Posso afirmar isto, pois em uma das aulas da Profª. Regina, no Curso de Especialização, discutimos este assunto, depois de termos feito uma comparação entre os dois (“Proposta Curricular” e “PCNs”) como tarefa.
A tabela nos mostra que os materiais didáticos mais usados pelos professores são o “Material Dourado”, o “Cartaz Valor Lugar”, palitos e materiais de sucata. Acredito que todos utilizem o quadro negro, lápis de cor, o próprio aluno, mas não acharam pertinente mencionar, por talvez acreditarem que estes já são inerentes ao processo. Os materiais usados pela maioria dos professores são ricos e, se bem utilizados, proporcionarão uma boa base matemática, pois propiciam a compreensão, pelo aluno, do que está sendo trabalhado. Por que será que não estou confiando no que a tabela mostra!?
Todos os professores utilizam-se da exposição oral da matéria para suas aulas, se a tabela mostrasse algo diferente disto, provavelmente não retrataria a verdade. Os “trabalhos em grupo” e as “pesquisas” enriquecem a aula e facilitam o aprendizado. Que bom que a maioria dos professores utiliza-se desses procedimentos.
Gostei de ver que todos os professores consideram também a “Participação e interesse nas aulas” como aspecto importante no processo de avaliação do aluno. Por esse resultado acredito que o aluno esteja sendo visto como único, e seus esforços estejam sendo levados em conta. Não é só a “nota” que está sendo considerada para a avaliação dos alunos.
O que me espantou no resultado desta tabela foi o fato de que somente 32% dos professores participantes consideram relevante o número de alunos aprovados, para a avaliação do seu próprio trabalho. Para mim, este é o aspecto mais importante, pois, se houver muita reprova comigo é porque eu preciso mudar minha maneira de ensinar, eles não estão se apropriando do conteúdo. O interessante é que a maioria absoluta dos professores assinalou “apropriação do conteúdo pelo aluno” como aspecto importante, como se isto não estivesse ligado à sua aprovação.
Fazendo um paralelo entre as duas tabelas, “Aspectos Dificultadores” e “Aspectos Facilitadores”, percebi que provavelmente, cada um tenha assinalado o que representa uma “dificuldade” ou uma “facilidade” para si próprio e não para qualquer professor, ou para o processo. Nesta linha de pensamento, 56% dos participantes consideram “faciltador” o fato de ter conhecimento do conteúdo inerente à série em que atua, mas nenhum deles considerou como “dificultador” não saber o conteúdo; somente um professor considera facilitador a “vontade do professor em querer que o aluno aprenda”, será que os demais professores se esqueceram de como é importante para todos que demonstremos o quanto queremos seu sucesso? Nenhum professor se considera desestimulado devido ao baixo salário que recebe, e somente três professores consideram “salário compatível e satisfatório” como aspecto facilitador, provavelmente, para os outros quarenta e sete professores o seu desempenho independe do salário que recebem; a maioria dos professores considera o “turno intermediário” como aspecto dificultador, eu que já trabalhei nesse horário, concordo que é um “dificultador” do trabalho de toda a escola; 52% dos professores participantes consideram a indisciplina dos alunos como aspecto dificultador, mas somente 32% consideram facilitador, não seria lógico os mesmos que consideraram dificultador a indisciplina considerassem a disciplina como facilitador? Que bom que as escolas municipais estão bem equipadas com materiais didáticos, a maioria dos professores considera esse aspecto facilitador de seu trabalho. Os 48% “em branco” na tabela de “dificultadores” referem-se aos professores que não consideraram aspecto dificultador algum. Uma pergunta me veio à mente: se a maioria dos professores quase não vê muitos aspectos dificultadores do seu trabalho, por que o índice de repetência é tão grande? Será que está ligado ao fato observado numa das tabelas anteriores na qual os professores não consideraram o número de alunos aprovados como aspecto relevante na avaliação de seu próprio trabalho!?
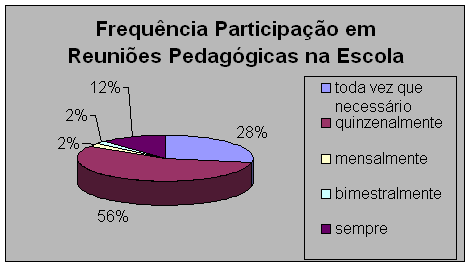
A tabela o gráfico nos mostram que a maioria dos professores participa de reuniões pedagógicas na escola quinzenalmente, isto se deve ao fato de na rede Municipal de Ensino ter “Grupo de Estudos”, geralmente de 15 em 15 dias, nos quais são discutidos assuntos pedagógicos, podendo ser conduzido pelo supervisor ou por convidados.
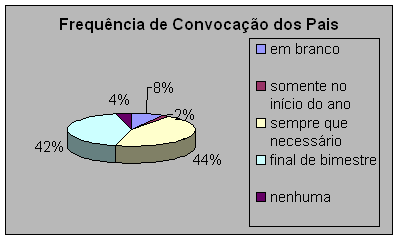
A tabela e o gráfico nos fazem ver que a maioria dos professores convoca os pais sempre que necessário, para discutirem questões a respeito do seu trabalho pedagógico. Provavelmente, esse sempre que necessário seja quando surgir algum problema ou alguma mudança drástica no trabalho pedagógico do professor.
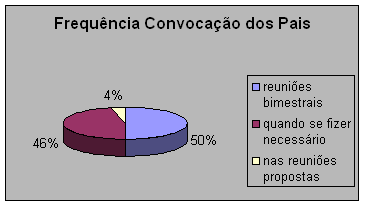
A tabela e o gráfico nos mostram que a metade dos professores participantes convoca bimestralmente os pais dos alunos para falar-lhes do desempenho escolar de seus filhos. Em todo meu tempo de escola, como aluna ou como professora, sempre foi assim e, acho que é o suficiente para a maioria dos alunos. O pai que é “presente” no processo escolar do filho, tem como acompanhar o desempenho dele por meio de diálogo com o filho, observando seu material, suas atividades e suas “provas” e sabe que tem o direito de procurar a escola sempre que quiser.
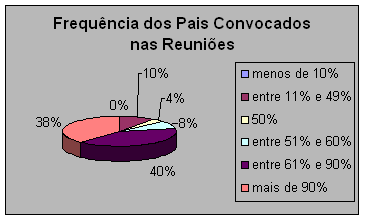
Observando o gráfico e a tabela, vemos que a participação dos pais nas reuniões pelas quais são convocados é muito boa, pois setenta e oito por cento dos professores participantes responderam que a maioria dos pais participa das reuniões. Este é um dado que me deixou feliz, pois os pais estão tomando consciência de que sua participação no processo escolar do filho é importante.
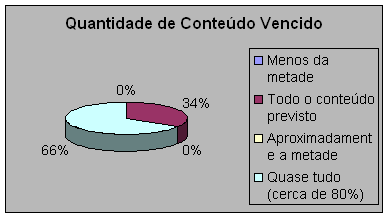
O gráfico e a tabela nos indicam que a maioria dos professores consegue cumprir quase todo o conteúdo previsto e somente trinta e quatro por cento dos participantes consegue cumprir todo o conteúdo previsto. Esse resultado pode ser positivo desde que, o professor priorize os conteúdos que ele julgue imprescindíveis para o processo escolar do aluno, e também tenha a oportunidade de colocar para o professor da série seguinte os conteúdos que não foram trabalhados. Para os alunos que saem da quarta série, o “quase tudo” pode ser mais perigoso, pois a maioria das escolas municipais só atende crianças até a quarta série, então, fica difícil conversar com o professor da série seguinte para dizer-lhe dos conteúdos que não foram trabalhados, mesmo porque, nesta etapa o aluno só leva da escola o histórico escolar e o boletim, já não são mais fichas de apropriação de conteúdos como na 1ª. e 2ª. séries.
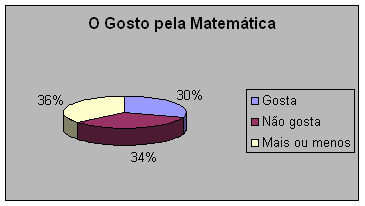
O gráfico e tabela nos mostram que somente 30% dos professores participantes gostam de matemática. Isto é uma pena, mas está bem ligado ao que mencionei quando abordei a “Formação de Professores”. Acredito que o “gosto” pela matemática deve ser trabalhado também nos professores, mas para tanto é necessário que o professor esteja aberto para enxergar a matemática sob um novo prisma. Este resultado me preocupou, pois não estou fazendo inferência sobre o assunto, é um fato que tem que ser trabalhado.
No questionário que utilizei para traçar o perfil dos participantes, pedi que justificassem sua resposta. A maioria dos professores que disseram não gostar de Matemática respondeu que não gostava pois no período escolar de quinta a oitava série e no Ensino Médio não tinha tido bons professores e são frutos de uma geração programada para “reproduzir” e não para raciocinar. Houve um professor que admitiu ter “traumas” até hoje em relação à Matemática. Os professores que disseram que gostam, justificaram dizendo que sempre tiveram facilidade com a matéria (talvez os “privilegiados”) e que a Matemática é uma necessidade em nossas vidas. Os que responderam que “gostam mais ou menos” disseram que na verdade preferem outras matérias, mas não fogem da Matemática.
Uma breve Descrição da Prova
As questões de uma prova podem ser classificadas quanto à forma de apresentação, quanto ao conteúdo e quanto ao tipo de problemas.
Quanto à forma de apresentação das questões podem ser:
a) Rotineiras – são questões que fazem parte do “dia-a dia” em sala de aula, exercícios comuns que aparecem com freqüência para serem resolvidos pelo aluno.
Exemplo:
Faça as operações indicadas e complete os espaços.
(A) 2,47 + 0,61 = _______ (B) 4,18 + 0,99 = _______ (C) 5,67 + 2,54 = _______
b) Intermediárias – são questões que aparecem no “dia- a- dia” em sala de aula, mas não com tanta freqüência.
Exemplo:
Houve uma gincana esportiva na escola para as 4ª. séries. Complete a tabela com o total de pontos de cada turma.
Turmas 1ª. Tarefa 2ª. Tarefa 3ª. Tarefa Total de Pontos 4ª. A 2125 1143 845 4ª. B 1875 2080 950 4ª. C 2400 2125 1000
c) Não – Rotineiras – são aquelas questões que raramente aparecem no dia- a- dia da sala de aula e, na maioria dos livros didáticos, aparecem como desafios.
Exemplo:
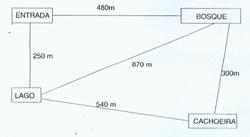
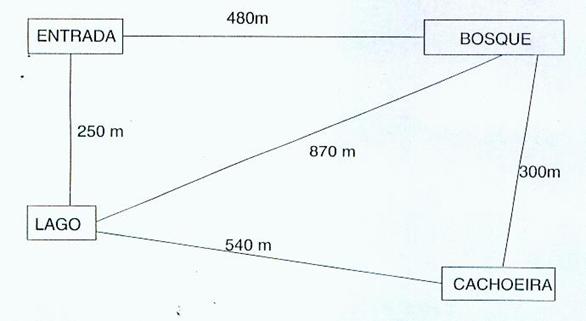
Veja o mapa de um parque florestal.
O caminho mais curto da entrada até a cachoeira mede _______________ e passa pelo ______________. A prova resolvida pelos professores está bem equilibrada em relação à “forma de apresentação” das questões. Na prova há um total de 30 questões, das quais eu julguei 10 rotineiras, 11 intermediárias e 9 não rotineiras.
Nas não rotineiras, incluí as que têm gráficos a serem analisados, pois sei que este tipo de questão, apesar de simples, não fazem parte do cotidiano da sala de aula, ou pelo menos não fazia em 1997.
Quanto ao conteúdo das questões
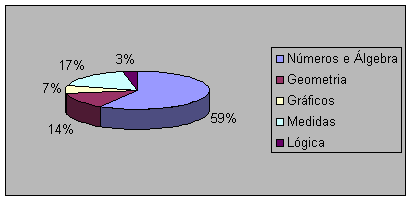
Na prova que analisei, mais ênfase foi dada a Numeração Decimal e Álgebra, uma vez que são os conteúdos que com mais freqüência são trabalhados pelos professores. Nela, 56,6 % das questões são relativas a Números e Álgebra, 13,3% relativas a Geometria, 16,6% relativas a Medidas, 3,3% relativas a Lógica e 6,6% relativas a Gráficos.
Quanto à classificação de tipos de problemas
“Na Resolução de Problemas, atual tendência da Educação Matemática, podemos classificar os” exercícios “em cinco categorias: exercícios de reconhecimento – são os que pedem apenas que o aluno reconheça ou relembre um fato, uma definição, etc; exercícios algorítmicos – são os que podem ser resolvidos através do uso de um algoritmo, ou procedimento passo-a-passo; problemas de aplicação – são os que precisam de mudança de linguagem escrita com palavras pra uma linguagem matemática adequada de modo que se possam utilizar os algoritmos apropriados; problemas em aberto – são os que não contêm no seu enunciado pista alguma para sua resolução; situações problemas – são aquelas nas quais a primeira coisa a fazer é identificar o problema inerente, cuja solução vai ajudar a “manejar” as próprias situações.” (BURIASCO, 1995 – p. 01)
Nesta concepção, temos que na prova resolvida pelos professores, 63,3% são exercícios de reconhecimento e algorítmicos.
Em uma das aulas do curso de Especialização, na qual a Profª. Regina falava sobre Avaliação, entramos no mérito da elaboração das provas constantes da Avaliação Estadual e, a Profª. Regina nos disse que os elaboradores (ela fez parte da elaboração das provas) pensavam sempre em elaborar uma prova que pudesse mostrar o que os alunos sabiam, portanto tinham de colocar questões com as quais eles tinham familiaridade, não podiam colocar outras dificuldades na prova senão as do próprio conteúdo, por esse motivo tanta ênfase na Álgebra e tantas questões “Rotineiras” envolvendo exercícios algorítmicos e/ou de reconhecimento, mas não podiam perder a oportunidade de mostrar ao professor uma maneira diferente de trabalhar, por isso, colocaram algumas questões “Não-Rotineiras”.
Analisando as questões
A partir da correção da prova, elaborei um resumo referente a cada questão.
Neste resumo você verá a questão propriamente dita, a maneira como foi apresentada, seu conteúdo, uma forma de resolução desta questão, os erros que os professores cometeram ao tentar resolvê-la e finalmente algumas considerações sobre os erros.
Nas considerações sobre o erro, levantei hipóteses que podem ter levado professor a cometê-lo, para tanto, tentei “pensar” como o professor pensou.
O ideal seria ter tido a oportunidade de questionar cada um em relação à sua resolução, mas isto não foi possível, pois o combinado foi que a identificação seria facultativa, e a maioria das provas estava sem identificação.
Analisando o “perfil dos participantes”, julguei que poderia realizar uma correção bastante criteriosa. Detalhe como “dois traços no cifrão” foi considerado erro .
1ª. Questão – Conteúdo: Adição
Houve uma gincana esportiva na escola para as 4ª. séries. Complete a tabela com o total de pontos de cada turma. Turmas 1ª. Tarefa 2ª. Tarefa 3ª. Tarefa Total de Pontos 4ª. A 2125 1143 845 4ª. B 1875 2080 950 4ª. C 2400 2125 1000
Resolução: 2125 + 1143 + 845 = 4113 1875 + 2080 + 950 = 4905 2400 + 2125 + 1000 = 5525
Erro encontrado 1 – Um professor “esqueceu” de somar o algarismo 3 da ordem das unidades na primeira adição, fez assim: 2125 + 1143 + 845 = 4110 1875 + 2080 + 950 = 4905 2400 + 2125 + 1000 = 5525 2ª. Questão – Conteúdo: Adição e Subtração
Paulo e Mariana têm juntos 2347 pontos num jogo. Quanto terão juntos se Paulo perder 379 e Mariana ganhar 413?
Resolução: 2347 – 379 = 1968 / 1968 + 413 = 2381 ou 413 – 379 = 34 / 2347 + 34 = 2381 Terão juntos 2381 pontos.
Erro encontrado 1 –Interpretação equivocada do problema
Três professores somaram a “perda” de Paulo com o “ganho” de Mariana e depois subtraíram do total de pontos que os dois tinham juntos. Esses professores acabaram subtraindo, então o que a Mariana havia ganho também. Fizeram assim: 379 + 413 = 792 2347 – 792 = 1555 Terão juntos 1555 pontos. 3ª. Questão – Conteúdo: Adição
Faça as operações indicadas e complete os espaços com os resultados. (A) 3128 + 16 + 490 = _______________ (B) 189 + 6184 + 5 = _______________ (C) 8 + 944 + 2007 = ________________
Resolução: (A) 3128 + 16 + 490 = 3634 (B) 189 + 6184 + 5 = 6378 (C) 8 + 944 + 2007 = 2959
Erro encontrado 1 – Um professor resolveu corretamente a adição do item (A), mas no local da resposta, trocou o algarismo 3 das dezenas pelo 8. Fez assim: (A) 3128 + 16 + 490 = 3684
Analisando o erro desse professor, percebi que provavelmente tenha sido apenas falta de atenção.
Erro encontrado 2 – Suponho que este professor tenha resolvido a operação mentalmente, pois na sua prova não há marca alguma referente à resolução desta questão, nela acabou invertendo as ordens da unidade e da dezena. (A) 3128 + 16 + 490 = 3643 Erro encontrado 3 –
Analisando todas as operações desta questão, notei que dois professores devem ter “esquecido” de somar o excedente da ordem das dezenas. Por isso atribuo a falta de atenção como causa desse erro. (B) 189 + 6184 + 5 = 6278 4ª. Questão – Conteúdo: Frações/Numerais decimais
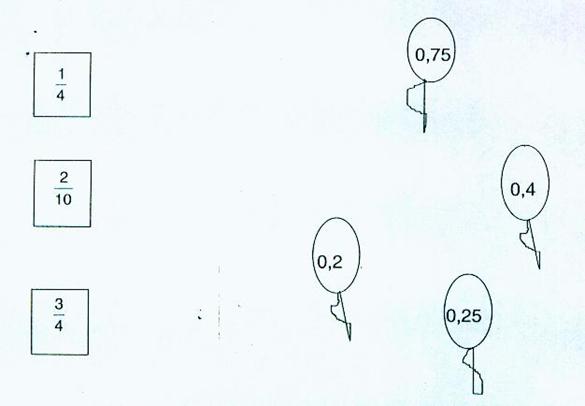
Ligue cada fração dos cartões abaixo ao número decimal correspondente nos balões.
Resolução: Ligar 1/4 com 0,25, 2/10 com 0,2, 3/4 com 0.75, deixando 0,4 do balão sem ser relacionado.
Erro encontrado 1 – Má compreensão do conteúdo
Dois professores relacionaram corretamente as frações 1/4 e 3/4, mas deixaram em branco o 2/10.
Analisando a resolução, levantei as seguintes hipóteses: - esses professores não compreendem “frações decimais” ou - não lembram como faz a transformação de fração para decimal e acertaram as duas por terem mais familiaridade com elas, ou - erraram ao fazer a divisão de 2 por 10, não encontrando assim um correspondente pra fração.
Erro encontrado 2 – Falta compreensão do conteúdo
Um professor relacionou corretamente as frações 2/10 e 1/4 , mas relacionou o 3/4 com o 0,4. Analisando a questão e a resolução, levantei a seguinte hipótese para o erro: - Esse professor relacionou corretamente somente as frações que ele já tem gravadas em sua memória, ele não compreende como fazer a transformação de fração para decimal.
5ª. Questão – Conteúdo: Área do Retângulo
Qual é a área de um campo que tem 12 metros de comprimento e 9 metros de largura?
Resolução: 12 x 9 = 108 A área é 108 metros quadrados.
Erro encontrado 1 – Não domina o conteúdo Dois professores calcularam o perímetro da figura ao invés da área, eles fizeram assim: Desenharam um retângulo, colocaram as medidas correspondentes e fizeram as seguintes operações: 12 x 2 = 24 24 + 18 = 42 R: A área é 42 m. Esses professores confundiram área com perímetro, portanto, eles não compreendem nenhum dos dois conceitos.
Erro encontrado 2 – Dez professores resolveram corretamente a questão, mas deram a resposta em “metros” e não em “metros quadrados”. Teria sido falta de atenção!? Será que eles, ou algum deles não compreende que no plano temos duas dimensões?!
Erro encontrado 3 –
Um professor resolveu corretamente a questão, mas deixou a resposta em branco. Será que esse professor não sabe
dar a resposta, e para não errar deixou em branco!? Será que esqueceu de dar a
resposta!? Será que ele não compreende a importância da resposta em um
problema!?
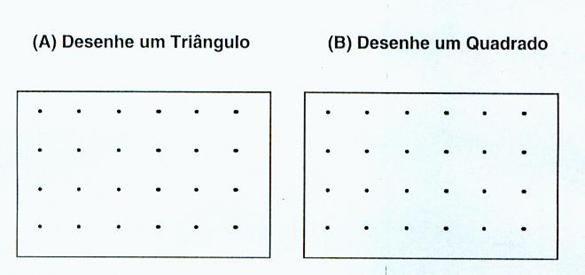
Ligue os pontos para desenhar as figuras geométricas.
Resolução: Ligar os pontos do item (A) e desenhar qualquer triângulo, pode utilizar os pontos como quiser, desde que se desenhe um triângulo, esse triângulo não tem tamanho ou posição determinados. e Ligar os pontos do item (B) e desenhar qualquer quadrado, não interessa o tamanho deste.
Erro encontrado 1 – Não percebe diferença entre quadrado e retângulo
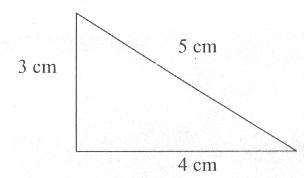
Dois professores desenharam em (B) um retângulo e não um quadrado. Possivelmente esses professores não sabem as propriedades de um quadrado, que são 4 lados iguais, 4 ângulos retos e lados opostos paralelos. Para eles, retângulo e quadrado são a mesma coisa. Existe também a hipótese deles terem achado que como todo quadrado é retângulo, a recíproca é válida, ou melhor, deles terem achado que todo retângulo também é quadrado, mas a recíproca não é verdadeira, pois para se ter um quadrado é necessário que todos os quatro lados sejam iguais e no retângulo isso não é uma condição. 7ª. Questão – Conteúdo: Perímetro Qual o perímetro da figura abaixo?
Resolução: Para calcular o perímetro de uma figura basta somar as medidas de seus lados. Assim, neste caso: 3cm + 5cm + 4cm = 12cm R: O perímetro é 12 cm.
Erro encontrado 1 – Três professores deixaram esta questão sem resposta, mas o cálculo que eles apresentaram estava correto. Por esse motivo, concluí que foi falta de atenção.
Questão em branco : Um professor deixou esta questão em branco. Será que ele não lembra ou não sabe o que é perímetro!? 8ª. Questão – Conteúdo: Equivalência de figuras planas
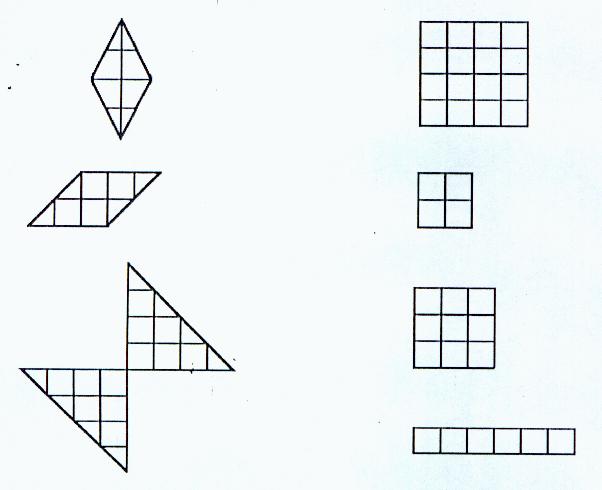
Ligue as figuras que possuem mesma área.
Resolução: Contando os “quadradinhos” de cada figura, ligar as que possuírem a mesma quantidade.Chamemos aqui as figuras da esquerda de (A), (B), (C) e as da direita de (1), (2), (3) e (4). Deveriam ser relacionadas às figuras (A) com (2), (B) com (4) e (C) com (1), a figura (3) ficaria sem ser relacionada.
Erro encontrado 1 – Não compreende o conteúdo Um professor ligou (A) com (2) e (B) também com (2), não ligando as demais figuras. Possivelmente, esse professor não saiba como descobrir a área dessas figuras para compará-las e, para não deixar em branco, ligou qualquer coisa. Ou, talvez ele não saiba o que é “área”.
Erro encontrado 2 – Um professor ligou corretamente as figuras (B) e (C), mas não relacionou a figura (A). Terá sido falta de atenção!? Talvez ele tenha calculado a área, mas erroneamente, não encontrou correspondente para essa figura.
Questão em branco : Três professores deixaram esta questão em branco. Penso que alguém deixa uma questão em branco quando não sabe resolvê-la, portanto falta conhecimento do conteúdo, e neste caso é importante que isto seja trabalhado. 9ª. Questão – Conteúdo: Subtração
Faça as operações indicadas e complete os espaços com os resultados.
(A) 4023 – 918 = ____________ (B) 9000 – 674 = ____________ (C) 3040 – 508 = ____________
Resolução: Fazer as subtrações cujos resultados são: (A) 4023 – 918 = 3105 (B) 9000 – 674 = 8326 (C) 3040 – 508 = 2532
Não foi encontrado erro nesta questão.
10ª. Questão – Conteúdo: Divisão
Faça as operações indicadas e complete os espaços com os resultados.
(A) 1250 ¸ 12 = ____________ (B) 3060 ¸ 9 = ____________ (C) 4791 ¸ 20 = ____________
Resolução:
Fazer as divisões cujos resultados são: (Não é preciso fazer a parte decimal) (A) 1250 ¸ 12 = 104,16667 (B) 3060 ¸ 9 = 340 (C) 4791 ¸ 20 = 239,55
Erro encontrado 1 – Não compreende o significado do “resto"
Um professor ao resolver a divisão (C), o fez corretamente até a ordem das unidades, o resto foi 11 (onze), mas ele quis continuar a conta e como onze não era divisível por 20, ele colocou “zero” no quociente, portanto, o quociente apresentado por esse professor foi 2.390. Assim:
(C)
4791 ¸ 20 = 2.390
Erro encontrado 2 -
Um professor deu o resultado 315,166 para a divisão (A), mas não posso determinar o que houve, pois ele não deixou os cálculos. (A) 1250 ¸ 12 = 315,166
Erro encontrado 3 – Dificuldade com o conteúdo
Um professor ao fazer a divisão (A) errou ao não considerar que não foi possível dividir a ordem das dezenas, portanto não colocou o “zero” no quociente, seu resultado foi 14 ao invés de 104 e, também não soube continuar a conta, veja abaixo.
Provavelmente esse professor tem problemas com a sua compreensão de “divisão”, pois ele nem mesmo fez uma estimativa do resultado, ele não percebeu que 1250 dividido por 12 daria pelo menos 100 como resultado.
Erro encontrado 4 -
Um professor errou na parte decimal do quociente da divisão (A). (A)
1250 ¸ 12 =104,1515 Esse professor, na parte centesimal de sua operação não percebeu que dividindo o “resto” 80 por 12 teria como quociente o número 6, logo o resto seria 8 e não 20 (número maior que o divisor) como ele colocou, ele também não percebeu que o 20 passou a ser resto e o dividiu de novo colocando o algarismo 1 na parte milésima de sua conta, logo esse professor dividiu o resto 80 nos centésimos e nos milésimos. O professor não percebeu que o resto 20 é maior que o divisor, e que seu quociente nos centésimos seria 6 e não 5 como ele colocou, o que pode significar falta de compreensão do algoritmo.
11ª. Questão – Conteúdo: Sistema de numeração decimal
Decomponha os números para completar os espaços em branco.
(A) 3428 = 3000 + 400 + 20 + _______ (B) 2376 = 2000 + 300 + ______ + ______ (C) 6551 = 6000 + _____ + _____ + _____ (D) 4739 = _____ + _____ + _____ + _____
Resolução: (A) 3428 = 3000 + 400 + 20 + 8 (B) 2376 = 2000 + 300 + 70 + 6 (C) 6551 = 6000 + 500 + 50 + 1 (D) 4739 = 4000 + 700 + 30 + 9
Erro encontrado 1 –
Um professor, no item (D), decompôs assim: (D) 4739 = 4000 + 700 + 39 + 9 Considerei como falta de atenção depois de analisar os outros itens dessa questão, feitos por esse professor, pois os demais estavam corretos.
12ª. Questão – Conteúdo: Subtração
Faça as operações indicadas e coloque os resultados nos espaços.
(A) 3632 – 97 = _________ (B) 1369 – 935 = ________
Resolução: Fazer as operações cujos resultados são: (A) 3632 – 97 = 3535 (B) 1369 – 935 = 434
Erro encontrado 1 – Um professor na operação (A) pareceu que “esqueceu” que uma das 6 centenas foram trocadas por dezenas, ficando somente 5 centenas e, seu resultado foi: (A) 3632 – 97 = 3635 Provavelmente tenha sido falta de atenção, mas não pude analisar o que foi feito, pois esse professor não deixou seus cálculos.
13ª. Questão – Conteúdo: Lógica
Ana, Carlos, Paulo e Sônia são quatro amigos que passaram nos quatro primeiros lugares de um concurso. Os primeiros lugares foram ocupados por meninos. Sônia não foi a quarta colocada. Carlos ficou melhor colocado do que Paulo. COMPLETE O PLACAR. 1º. Lugar ___________________ 2º. Lugar ___________________ 3º. Lugar ___________________ 4º. Lugar ___________________
Resolução: 1º. Lugar: Carlos 2º. Lugar: Paulo 3º. Lugar: Sônia 4º. Lugar: Ana
Não foi encontrado erro nessa questão.
14ª. Questão – Conteúdo: Multiplicação
Faça as operações indicadas e complete os espaços com os resultados.
(A) 407 x 32 = ______________ (B) 629 x 40 = ______________ (C) 245 x 56 = ______________
Resolução: Resolver as operações cujos resultados são: (A) 407 x 32 = 13 024 (B) 629 x 40 = 25 160 (C) 245 x 56 = 13 720
Erro encontrado 1 –
Um professor ao copiar a multiplicação do item (A), para resolvê-la, traçou o “zero” do 407 com defeito e ele ficou parecendo um “seis” então, ele resolveu a operação como se fosse 467 x 32. (A) 407 x 32 = 14 944 15ª. Questão – Conteúdo: Multiplicação
O jornal da escola tem 12 páginas de 4 colunas cada uma. Uma coluna contém 55 linhas. Quantas linhas tem o jornal todo?
Resolução: 12 x 4 = 48 colunas 48 x 55 = 2640 linhas R: O jornal todo tem 2640 linhas.
Erro encontrado 1 – Resposta incompleta
Nove pessoas resolveram corretamente o problema, mas deram a resposta incompleta, somente com o 2640. Como o problema tratava de linhas e colunas, é importante especificar 2640 linhas, pois, poderia ser “colunas”.
16ª. Questão – Conteúdo: Numeração decimal
Veja os valores dos símbolos.
Resolução: Chamemos, de cima pra baixo, os itens respectivamente de (A), (B), (C). Então teremos que: (A) vale 2321 (B) vale 1503 (C) vale 3116
Erro encontrado 1 –
Um professor no terceiro item dessa questão considerou o “quadradinho” como 10, usando duas ordens para colocá-lo, a dezena e a centena e seu resultado foi: (C) vale 31106.
Erro encontrado 2 –
Um professor no terceiro item dessa questão considerou o símbolo que vale 100 como 200 então sua resposta foi: (C) vale 3216
Em ambos os casos, atribuo o erro à “falta de atenção” pelo fato do erro não ter persistido em todos os itens, mesmo porque esses dois erros foram encontrados em provas distintas.
17ª. Questão – Conteúdo: Fração
Qual a fração que representa a parte pintada da figura abaixo?
Resolução:
Como é uma figura “dividida” em três partes e duas delas estão pintadas, então a fração que representa a parte pintada é 2/3.
Erro encontrado 1 –
Duas pessoas consideraram a parte em branco da figura e não a parte pintada, então, a resposta foi: 1/3.
Analisando a resposta dada por esses professores, penso que eles não tenham dado a devida atenção ao enunciado, ou não entenderam o que foi pedido, ou não se apropriaram do conhecimento necessário.
Erro encontrado 2 – Má interpretação da questão
Duas pessoas completaram a figura, transformando-a num retângulo e, consideraram a parte pintada do retângulo que elas obtiveram. A resposta dada foi: 2/4.
Pelo fato destes professores terem completado a figura, acredito que eles não tenham entendido a questão. Analisando suas respostas vemos que, de acordo com o que eles pensaram, a resposta está certa, mesmo assim, penso que estes professores tenham problemas na compreensão de “frações”, pois eles não estão conseguindo “enxergar” representações de frações em quaisquer figuras.
18ª. Questão – Conteúdo: Medida de comprimento
Veja o mapa de um parque florestal.
Resolução: Somar as distâncias dos caminhos propostos, compará-los e decidir qual é o menor.Um dos caminhos, mede 780m e passa pelo bosque, outro caminho mede 790m e passa pelo lago e, o caminho pela diagonal mede 870m, como mostra a figura, então a resposta a esta questão é: O caminho mais curto de entrada até a cachoeira mede 780m e passa pelo bosque.
Erro encontrado 1 –
Doze pessoas esqueceram de colocar a unidade de medida na resposta, colocaram apenas 780.
Provavelmente, tenha sido apenas “falta de atenção”.
19ª. Questão – Conteúdo: Sistema métrico decimal
Cortei 155 centímetros de um barbante de 3 metros, quanto sobrou?
Resolução: Tem de fazer uma transformação de medidas, ou o 155cm em metros ou o 3m em centímetros. Assim: 155cm = 1,55m 3,00m – 1,55m = 1,45m ou
3m = 300cm 300cm – 155cm = 145cm R: Sobrou 1,45m ou 145 cm.
Erro encontrado 1 – Uma pessoa não colocou a unidade de medida em que trabalhou e respondeu somente: 145.
Possivelmente esse professor tenha feito os cálculos mentalmente e não deu a devida atenção às unidades de medidas do problema, pois essa resposta poderia ser dada em metros ou em centímetros. Outra hipótese a ser levantada é a de ele não ter certeza de qual unidade usaria na resposta.
Erro encontrado 2 – Uma pessoa resolveu corretamente a questão em metros, mas passou a resposta errada assim: 3,00 – 1,55 = 1,45 R: 2,45m Atribuo esse erro somente á falta de atenção.
Erro encontrado 3 – Uma pessoa resolveu a questão assim: 300 – 155 = 1,45 e, deixou a questão sem resposta.
Possivelmente esse professor tenha problemas com a compreensão do sistema de medidas, o fato dele ter deixado sem resposta pode mostrar que ele tem dúvidas a respeito do que fez.
Erro encontrado 4 –
Um professor transformou o “3 metros” em milímetros, mas não transformou o “155 centímetros” em milímetros também. Fez assim: 3000 – 155 = 2 845
R: Sobrou 2.845.
Esse professor provavelmente tenha dúvidas em relação às equivalências no sistema métrico decimal, pelo que pude notar, pra ele, 1m corresponde a 1000 centímetros, por isso ele não transformou o 155. Outra hipótese a ser levantada é a
de ter sido apenas “falta de atenção” ao ler e resolver o problema, talvez se o
professor tivesse relido o problema para dar a resposta, ele percebesse seu
erro.
Qual é a porcentagem da tabela abaixo que já está pintada?
Resolução: A figura em questão está dividida em 100 pedacinhos iguais e 74 deles estão pintados, então a resposta é 74%.
Não foi encontrado erro nesta questão.
21ª. Questão – Conteúdo: Porcentagem
Das 200 crianças de uma creche, 50 tem menos de 4 anos. Qual a porcentagem das crianças com menos de 4 anos?
Resolução: Uma das maneiras é “pensando assim” e foi a que mais apareceu nas provas. Quantos 50 cabem no 200? Cabem 4 vezes o 50, então 50 crianças corresponde a 25% do total R: A porcentagem é 25%
Erro encontrado 1 – Resposta Um professor deixou a questão sem resposta.
22ª. Questão – Conteúdo: Subtração / Medida de comprimento
Um ônibus levando 40 passageiros fará uma viagem de 1430 quilômetros. Quantos quilômetros faltam para terminar a viagem se o ônibus já percorreu 385 quilômetros?
Resolução: Esse problema traz um dado que não será utilizado. Basta calcular a diferença entre 1430km e 385km, assim: 1430 Km – 385 Km = 1045 Km R: Faltam para terminar a viagem. 1045 quilômetros.
Erro encontrado 1 – Resposta Quatro professores não colocaram a unidade de medida em sua resposta, responderam apenas 1045.
Erro encontrado 2 – Dois professores erraram ao resolver a subtração, esqueceram de “abaixar” o algarismo “1” da ordem das unidades de milhar do número 1430. Fizeram assim: 1430 – 385 = 45 R: Faltam 45 quilômetros.
23ª. Questão – Conteúdo: Gráficos
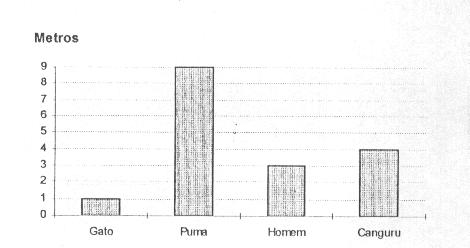
O gráfico abaixo mostra a altura que alguns animais conseguem pular.
Pode-se dizer que (A)
o
animal que pula mais alto (B) o puma pula ________ metros a mais que o homem. (C) O gato pula ________ metros a menos que o canguru.
Resolução: Observando o gráfico atentamente resolve-se corretamente a questão. (A) o animal que pula mais alto é o puma (B) o puma pula 6 metros a mais que o homem. (C) O gato pula 3 metros a menos que o canguru.
Não foi encontrado erro nesta questão.
24ª. Questão – Conteúdo: Medida de comprimento
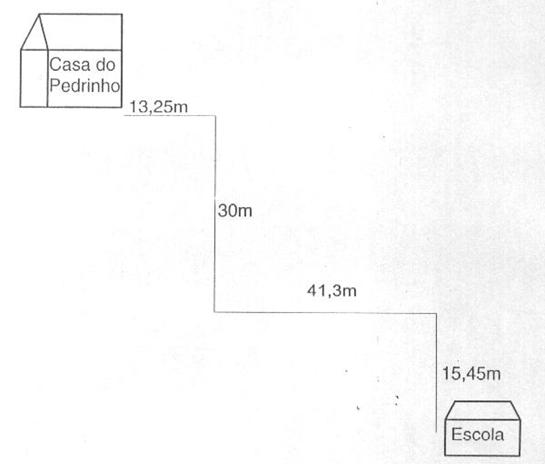
Siga o roteiro do mapa. Quantos metros Pedrinho tem que caminhar para chegar a escola?
Resolução: Somar as distâncias indicadas. 13,25m + 30,00m + 41,30m + 15,45m = 100m R: Pedrinho tem que caminhar 100m para chegar a escola.
Erro encontrado 1 – Notação de medida.
Três professores resolveram corretamente, mas a resposta foi: R: 100 mts Provavelmente esses professores não sabem que as abreviações de medidas não têm plural. Por exemplo, para se abreviar 100 gramas, o correto é 100g e não 100 grs., para se abreviar 100 metros, o correto é 100m e não 100 mts. Para comprovar isto é só pegar embalagens diversas e observar suas capacidades. Esta notação, sem plural, vale também para “horas”, nas quais se utiliza somente o “h” assim: 10h (10 horas) e não 10 hrs, ou 10H. 25ª. Questão – Conteúdo: Divisão/ Medida de tempo
Uma semana tem 7 dias e um ano tem 365 dias. Um ano tem quantas semanas?
Resolução: 365 ¸ 7 = 52 com resto 1 R: Um ano tem 52 semanas.
Erro encontrado 1 – Falta de resposta
Uma pessoa resolveu corretamente a questão, mas deixou a resposta em branco.
Neste caso, como a prova estava com a identificação de quem a tinha feito, pude conversar com o professor a respeito de seu erro. Ele me disse que achou que não precisasse da resposta, que não tivesse importância. Eu aproveitei e falei da importância da resposta que neste caso, com uma mesma operação, poderiam ter sido feitas diferentes perguntas. Por exemplo, poderia ter sido feita uma pergunta na qual a resposta fosse o “resto”, no caso, o 1 dia que sobrou. O professor disse que não havia pensado nisso e que a partir de agora daria mais atenção à resposta dos problemas e enfatizaria isso com seus alunos. 26ª. Questão – Conteúdo: Gráfico
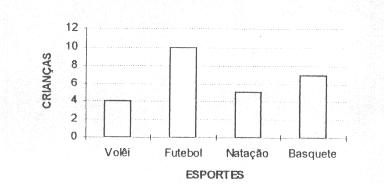
Este gráfico mostra a preferência das crianças da 5ª. Série B por esportes.
(A) O esporte que as crianças menos gostam é ________ (B) O total de crianças que gosta de futebol é __________
Resolução: Observando o gráfico em questão com atenção temos: (A) O esporte que as crianças menos gostam é o Vôlei (B) O total de crianças que gosta de futebol é 10
Erro encontrado 1 – Um professor completou o item (B) assim: (B) O total de crianças que gosta de futebol é 30 Analisei esta resposta por diversas maneiras, mas não consegui encontrar uma causa para esse erro, pelo que pude notar, nada levaria a responder 30 a essa pergunta. Nem tem 30 alunos na série em questão! 27ª. Questão – Conteúdo: Comparação de numerais
Complete os espaços com os sinais que se encontram no quadro. > maior que > menor que = igual a
(A) 603 _____ 498 (B) 240 _____ 420 (C) 670 – 170 _____ 400 + 100 (D) 5 x 200 _____ 100
Resolução:
(A) 603 > 498 (B) 240 <420 (C) 670 – 170 = 400 + 100 (D) 5 x 200 > 100
Não foi encontrado erro nesta questão.
28ª. Questão – Conteúdo: Adição de numerais decimais
Faça as operações indicadas e complete os espaços.
(A) 2,47 + 0,61 = _______ (B) 4,18 + 0,99 = _______ (C) 5,67 + 2,54 = _______
Resolução:
(A) 2,47 + 0,61 = 3,08 (B) 4,18 + 0,99 = 5,17 (C) 5,67 + 2,54 = 8,21
Erro encontrado 1 –
Um professor, no item (A) fez a operação de subtração ao invés da soma. (A) 2,47 + 0,61 = 1,86 Analisei como sendo falta de atenção, pois os demais itens ele fez acertadamente.
29ª. Questão – Conteúdo: Sistema monetário
Rogério comprou 7 cadernos de R$ 0,80 cada um. Para facilitar o troco pagou com R$ 10,60. Qual foi o troco?
Resolução: 0,80 x 7 = 5,60 10,60 – 5,60 = 5,00 R: O troco foi R$ 5,00.
Erro encontrado 1 – Notação de medida
Treze professores colocaram dois traços no $ Esse tipo de erro é comum, pois o cifrão com dois traços já foi utilizado em nosso sistema monetário, provavelmente esses professores não se deram conta de que atualmente usamos o cifrão somente com um traço.
Erro encontrado 2 – Um professor resolveu corretamente a multiplicação, mas errou a subtração, assim: 0,80 x 7 = 5,56 10,60 – 5,60 = 5,60 R: O troco foi R$ 5,60 Provavelmente tenha sido somente falta de atenção.
Erro encontrado 3 – Resposta
Um professor não colocou o “R$” na resposta. Assim: O troco foi 5,60. Talvez esse professor não considere importante a unidade de medida na resposta, mas esta é de suma importância porque nos mostra a natureza do objeto do qual o problema trata.
30ª. Questão – Conteúdo: Sistema de numeração decimal
Quanto vale o algarismo 3 em cada um dos números abaixo? 1361 ¯ _________ unidades
1631 ¯ _________ unidades
3226 ¯ _________ unidades
6213 ¯ _________ unidades
Resolução: Chamemos respectivamente, de cima para baixo, os itens dessa questão de (A), (B), (C), (D). Em (A) o algarismo 3 vale 300 unidades Em (B) o algarismo 3 vale 30 unidades Em (C) o algarismo 3 vale 3000 unidades Em (D) o algarismo 3 vale 3 unidades.
Não foi encontrado erro nesta questão.
Apresentarei a seguir duas tabelas, em uma delas colocarei o número de erros ocorridos em cada questão e na outra, assinalarei as questões que cada professor errou. Estas tabelas permitirão que visualizemos a questão em que o índice de erro foi maior e o número de erros que cada professor cometeu.
As questões que os professores mais erraram foram as de número 5, 18 e 29. A questão de número 5 envolveu área de um retângulo, mas os professores erraram mais ao darem a resposta, não utilizaram o “metro quadrado” e sim o “metro” simples; a questão 18 envolveu medida de comprimento e, o erro dos professores foi não colocar a unidade de medida na resposta, talvez porque considerem irrelevante; a questão de número 29 tratava de “sistema monetário”, que também é uma medida, só que de valor e os professores utilizaram dois traços para o cifrão e não um que é o correto. O índice de erro da questão quinze também foi grande e, novamente o problema residiu na resposta incompleta.
O que me chamou a atenção, foi esse “descaso” dos professores em relação à resposta dos problemas. Se eles agem assim, provavelmente devam passar isso para o aluno. Não é que eu ache que só a resposta importa, mas com certeza ela também é importante na resolução de um problema. É a busca da resposta que nos levará a traçar o caminho a ser seguido.
Observando a segunda tabela, você verá que somente dois professores acertaram a prova toda.
Tabela 24 – Distribuição de Acertos, Erros e Brancos
Legenda: X ® Erro na Questão / à ® Questão em Branco Algumas sugestões
Analisando os erros cometidos, percebi que muitos deles estão ligados ao “Sistema Métrico Decimal”, então vamos dar uma atenção especial à esse conteúdo.
1. Como surgiu o “metro” ?
O metro constitui a unidade básica de comprimento do Sistema Métrico decimal, adotado pela maior parte dos países, conseguindo-se assim um método uniforme de medidas, que eliminou a confusão existente neste setor. Esta confusão no sistema de pesos e medidas constituía uma herança da Idade Média e do Feudalismo, pois cada senhor feudal tinha suas medidas, e, mesmo depois de se ter processado a centralização monárquica nos países do ocidente europeu, os monarcas não conseguiam impor uma unificação.
Assim, em fins do século XVIII, havia na França cerca de duzentas unidades diferentes para medir comprimentos e distâncias, fato que ocorria também nos demais países do Ocidente.
Foi o governo revolucionário francês que tomou a iniciativa de eliminar esta situação. Em 1790, a Assembléia Constituinte francesa formulou um amplo projeto de unificação dos pesos e medidas. Algum tempo depois, a Academia das Ciências de Paris nomeava uma comissão de cientistas para estudar o problema e, esta comissão estabeleceu que:
1- era necessário adotar uma unidade de comprimento, derivada das dimensões da terra, que pudesse ser aceita por todos os países, bem como reconstituída a qualquer momento, no caso de se perder o padrão correspondente;
2- todas as unidades de superfície (área), volume, etc. derivariam desta unidade fundamental, que receberia o nome de “METRO” (do grego metron, medida);
3- todos o múltiplos e submúltiplos seriam formados segundo a numeração decimal, isto é, de dez em dez.
Visando cumprir o primeiro dos objetivos propostos, a comissão resolveu utilizar a medição de um arco de meridiano terrestre. Foi escolhido aquele que passa por Paris. Efetuaram-se então trabalhosas tarefas de medição, que foram prolongadas até a Costa da África. Ficou assim determinado o quadrante desse meridiano, isto é, a linha que vai do Pólo Norte ao Equador. A referida distância foi dividida em dez milhões de partes e se adotou uma unidade de comprimento daí resultante, consagrando-se pois o “METRO” como a décima - milionésima parte de um quadrante do meridiano, a temperatura de zero grau centígrado.
Na segunda metade do século XIX, efetuaram-se estudos mais precisos sobre o assunto, ficando demonstrado ter havido um pequenino erro no cálculo inicial, todavia decidiu-se manter a unidade anterior, que é dois décimos de milímetros inferior à cifra exata.
O “METRO” é a unidade fundamental do sistema legal de pesos e medidas; “METRO CÚBICO” é unidade de volume, correspondente a um cubo cujas arestas têm um metro de comprimento; “METRO QUADRADO” é unidade de área, é a área de um quadrado cujo lado tem um metro de comprimento.
Para a criança, é interessante que ela compreenda a necessidade de uma medida padrão, medindo com as mãos, com os dedos, com os pés, etc. Na classe, já aparecerá diferentes medidas para um mesmo objeto, pois as crianças têm tamanhos diferentes de pés, mãos, dedos... A situação será de impasse, dentre as diferentes medidas obtidas, qual deverá ser escolhida? Mesmo que a classe entre num acordo, será que alguém que não pertença à classe entenderá ou aceitará essa medida? É o momento de explicar sobre a necessidade de uma medida padrão, contar um pouco da história do metro e introduzir o metro como unidade fundamental de medida de comprimento. É importante que se apresente o “tamanho” do metro para o aluno utilizando um pedaço de barbante com um metro de comprimento e também instrumentos específicos como a fita métrica, o metro articulado de madeira e a trena. A necessidade de “dividir” o metro, ou seja, descobrir seus submúltiplos, também deve ser descoberta pelos alunos a partir de situações de medidas vivenciadas por eles. Para tanto, podemos pedir que meçam, utilizando um metro objetos pequenos como o caderno, a carteira, a borracha, o lápis, enfim, o que eles quiserem medir. Nesses casos, eles terão como resultado de medida “partes” do metro e, provavelmente alguns deles não saibam como dar a resposta, outros talvez saibam por já trazerem esse conhecimento consigo. Podemos dizer que essas situações também aconteciam antigamente e resolveram então, dividir o metro em “pedaços” menores, não creio que devamos simplesmente dizer os nomes dos submúltiplos e suas medidas, isso não os levaria à compreensão do conteúdo, sugiro então que para introduzirmos o decímetro, o centímetro e o milímetro trabalhemos uma atividade que leve o aluno a esse conhecimento.
Apresentarei a seguir algumas sugestões de atividades. Estas atividades também podem ser trabalhadas em uma “oficina” para professores.
São elas: Dividindo o metro O Perímetro Aprendendo a calcular áreas de quadrados e retângulos
Em seguida farei umas considerações sobre o “metro quadrado”, a falta de resposta nas questões, o cifrão e a falta de atenção, pois como já mencionei em páginas anteriores, foram causas de erros de muitos dos professores participantes.
Dividindo o metro ( “Atividades Matemáticas – 4ª. série do 1º. Grau” – Secretaria de estado da Educação – SP, 1194)
“Objetivo: introduzir os seguintes submúltiplos do metro: decímetro, centímetro e milímetro.
Material necessário: um pedaço de barbante de um metro e outro de dez centímetros.
Desenvolvimento:
1ª. Parte: Divida a classe em grupos de 4 alunos. Forneça a cada aluno um pedaço de barbante de 1m e outro pedaço de 1dm . Os alunos saberão apenas que o pedaço maior tem medida 1m, desconhecendo a medida do pedaço menor.
Levante as seguintes questões:
a) quantas vezes o pedaço de barbante menor cabe no pedaço de um metro?
b) represente com um número a parte do pedaço menor de barbante.
Como o pedaço de barbante menor cabe 10 vezes em 1m, dizemos, então, que sua medida é 1/10 de um metro. Introduza o termo decímetro, estabelecendo então as relações: 1dm = 1/10m e 1m = 10 dm.
2ª. Parte:
A proposta agora é pedir aos alunos que meçam o comprimento de objetos como: lápis, tampo da carteira, capa do caderno, etc; mostrando a necessidade da subdivisão do decímetro.
Primeiramente eles deverão medir utilizando apenas o pedaço de barbante de 1dm, indicando, por exemplo que o comprimento da capa do caderno mede 2 decímetros mais um pedaço de decímetro.
Introduzir, em seguida, o centímetro (cm) como a décima parte do decímetro e as relações: 1cm = 1/10dm e 1dm = 10cm
Utilizando a régua, eles podem determinar novamente as medidas dos mesmos objetos indicando a resposta, da maneira: 2 decímetros mais 3 centímetros ou ainda 2 x 10 + 3 = 23cm.
Colocar a questão: um metro tem quantos centímetros?
Os alunos deverão chegar às relações: 1m = 100cm e 1cm = 1/100m.
Como exercício, cada aluno deverá expressar sua altura em centímetros.
3ª. Parte:
Analisando a régua, os alunos verificarão que cada centímetro é dividido em 10 partes iguais.
Introduza o termo milímetro (mm) e discuta com a classe as relações: 1cm = 10mm, 1mm = 1/10cm, 1m = 1000mm e 1mm = 1/1000m.
Propor , ainda, para os alunos a questão: um decímetro tem quantos milímetros?”
Para introduzirmos o “quilômetro” como unidade para medir grandes distâncias, podemos, dando continuidade a atividade anterior, colocar na lousa questões do tipo:
1) Das unidades de medida de comprimento padronizadas que você conhece: o metro, o decímetro, o centímetro e o milímetro, qual delas é mais adequada para determinar:
a) o comprimento da sala de aula? b) o comprimento do seu lápis? c) o comprimento de uma formiga? d) a sua altura? e) a espessura de uma régua? f) a largura do seu caderno?
2) Você acha que o metro é uma unidade de medida adequada para dar a distância entre duas cidades? Por quê?
Após as discussões, a conclusão deverá ser que o metro não é uma unidade adequada para medir a distância entre duas cidades. É o momento de dizer que, assim como existem unidades menores que o “metro” para medir pequenos comprimentos, também existem unidades maiores que o “metro”, usadas para medir grandes distâncias. Uma delas, a mais usada, é o “quilômetro” (Km), que vale 1000 metros.
Para ilustrar o que foi discutido e concluído, os alunos poderão fazer uma pesquisa para determinar a distância entre várias cidades. A escolha das cidades pode ser determinada pelos alunos, alguma cidade que queiram conhecer, a capital do Brasil, uma cidade que achem bonita, a cidade onde moram seus parentes, etc.
Nas aulas que se seguirem, poderão ser apresentados problemas, como por exemplo:
1) Um viajante percorreu 45 200m no primeiro dia de viagem, 100Km no segundo dia e no terceiro dia percorreu 55 700m. Quantos quilômetros este viajante percorreu ao todo?
2) Que automóvel é mais econômico: um que gasta 10 litros de gasolina a cada 120Km ou outro que gasta 20 litros a cada 240 000m?
Outros problemas poderão ser elaborados pelos alunos, em grupos ou individualmente, e trocados entre a classe para que sejam discutidos e resolvidos.
O Perímetro
Objetivo: introduzir o conceito de perímetro.
Material necessário: um elástico de dinheiro e um geoplano.
Desenvolvimento:
Dispor a classe em grupos de 4 a 5 alunos. Entregar a cada grupo um geoplano e um elástico.
1ª. Parte: proponha aos alunos que utilizando o elástico, construam o menor quadrado possível, de modo que os vértices da figura fiquem determinados nos preguinhos. Peça-lhes que meçam os lados do quadrado e determinem o comprimento do elástico que foi utilizado. Em seguida, proponha que construam o maior quadrado possível. Novamente peça-lhes que determinem o comprimento do elástico que foi utilizado. Cada grupo deverá apresentar a maneira como descobriu o comprimento do elástico que foi utilizado. É neste momento que se define o perímetro como sendo a soma das medidas dos lados de uma figura. O comprimento utilizado do elástico é o perímetro do quadrado em questão.
2ª. Parte: peça aos alunos que construam outras figuras e determinem o perímetro de cada uma delas. É importante que se faça o registro do que está sendo feito. 3ª. Parte: desafie os alunos a construírem figuras diferentes que tenham o mesmo perímetro.
· Proponha aos alunos que encontrem no dicionário o significado da palavra “perímetro” e discuta o que foi encontrado.
· É importante relacionar sempre o “perímetro” com o “comprimento” para que mais tarde não haja “confusão” com o conceito de “área”.
Converse com os alunos sobre as aplicações do “Perímetro”. Colocar situações reais nas quais se precisa deste conceito como por exemplo: comprimento de arame suficiente para cercar terrenos, comprimento de madeira necessário para se fazer rodapés, etc.
Para construir o “Geoplano”, utilize um retângulo de madeira; desenhe sobre ele um quadriculado e coloque a seguir preguinhos nas intersecções das linhas. Os próprios alunos podem construir os geoplanos.
“Área: A OCUPAÇÃO DA TERRA
Desde os tempos mais antigos até os dias de hoje, a ocupação da terra para plantar, produzir, morar tem sido uma preocupação do homem que a ocupa e dos Governos que permitem essa ocupação.
Se os antigos egípcios pagavam impostos ao faraó, hoje pagamos à Prefeitura de cada município.
O imposto depende da área e da localização do terreno. Ele é calculado por metro quadrado.
Por essa razão, o cálculo de área sempre teve um papel importante na vida do homem.”(MORI; ONAGA, 1998, p.252)
Aprendendo a calcular áreas de quadrados e retângulos
Objetivo: introduzir o conceito de área; calcular, utilizando lado vezes lado, a área de figuras quadrangulares e retangulares.
Material necessário: folha quadriculada.
Desenvolvimento: Disponha os alunos em grupos.Entregue uma folha quadriculada a cada grupo e peça que desenhem um retângulo nesta folha. Cada grupo poderá desenhar o retângulo do tamanho que quiser. Peça-lhes então que determinem quantos quadradinhos pertencem ao retângulo que eles desenharam. Em seguida, proponha que contem os quadradinhos utilizados na base e na altura do retângulo, encontrando uma relação entre a quantidade de quadradinhos do retângulo todo e a quantidade de quadradinhos dos lados.
2ª. Parte: discuta com os grupos as relações que eles determinaram, peça que eles expliquem como chegaram a essa conclusão.
3ª. Parte: Repita a atividade, pedindo que desenhem outros retângulos, em seguida, repita com quadrados.
4ª. Parte: peça-lhes que comparem as relações que determinaram e verifiquem se elas são válidas sempre. Em seguida, diga-lhes que a quantidade de quadradinhos que cada figura utilizou é a área desta figura, tendo como unidade o “quadradinho” da folha e que, como eles descobriram, basta multiplicar lado (base) por lado (altura) para determinar quantos quadradinhos foram utilizados, ou seja, para determinar a área dessas figuras.
· Proponha aos alunos que encontrem no dicionário o significado da palavra “área” e discuta o que foi encontrado. · Discuta com os alunos a diferença entre “perímetro” e “área”.
O “metro quadrado”
O “metro quadrado” (m2) é a unidade padrão de medida de área e, consiste em um quadrado cujo lado mede um metro (1m), portanto sua área é um metro quadrado, pois como vimos na atividade anterior, para se calcular a área de um quadrado basta multiplicar a base pela altura e no quadrado elas são iguais, medindo 1m cada uma, então temos 1m x 1m = 1m2.
Para os alunos é importante que eles visualizem o “metro quadrado”, assim como “visualizaram” o tamanho do metro, para tanto, sugiro que seja construído, com os alunos, um quadrado com 1m de lado e calculada a sua área. A seguir, sugiro que seja feita a comparação do “metro” (simples) com o metro quadrado, pegue um barbante medindo 1m e coloque os dois (metro quadrado e metro simples) lado a lado depois, sobreponha-os. É importante que os alunos notem o “tamanho” (gravidade) do erro que cometeriam se, por acaso, usassem um no lugar do outro. Já que o metro quadrado está construído, seria muito proveitoso que os alunos descobrissem quantos desse quadrado cabem em sua sala de aula, descobrindo assim a área da sala de aula, depois, poderiam utilizar o barbante de um metro para medir os lados da sala e assim calcular a área da sala, fazendo lado vezes lado para comparar os resultados obtidos.
Falta de Resposta
Analisando as provas dos professores participantes, notei que um erro comum entre eles foi a “falta de resposta” às questões, erro este que eu considero muito sério, pois a “resposta” é a solução do problema, é ela que queremos, é por ela que seguimos determinado caminho, é ela que buscamos.
Penso que o crescimento vem da busca de respostas em nossas vidas, por exemplo, o avanço científico gira também em torno da busca de respostas, existe vida fora da Terra? Para a obtenção dessa resposta são gastos bilhões de dólares, já imaginaram se quando chegarem a uma resposta eles não nos contarem!? Outro exemplo, a cura do câncer, é uma busca de todo o planeta, o que nos interessa neste caso, a descoberta da própria cura, portanto a resposta, claro que o “como” foi descoberta esta resposta também interessa.
Vocês podem estar pensando, “Ah, mas ela mudou de assunto, não é deste tipo de resposta que estamos falando!”, é que para mim “resposta” é “resposta”, seja ela da natureza que for, se há pergunta, deve haver resposta. O resultado de uma conta, sozinho, não diz nada, há muitos “problemas” envolvendo várias operações, e se o problema estiver sem resposta, qual delas nos fornece a resposta? Mesmo que haja somente uma operação, talvez a resposta não seja o resultado dela e sim o “resto”, se tratando de uma divisão. Para o aluno acredito ser importante que ele pense como eu, resposta é resposta, e ela deve “combinar” com a pergunta, se a pergunta se referir a área, a resposta deverá vir em uma unidade de área, ou quando você pergunta o “nome” de uma pessoa você se satisfaria com a resposta, por exemplo, 35 anos!? É a mesma coisa, se a pergunta foi qual a área, você não pode responder “perímetro”.
Muitos dos professores participantes fizeram as respostas incompletas, ou seja, omitiram a “unidade” na mesma. Na linguagem oral, é comum essa omissão, mas a linguagem escrita exige um pouco mais de rigor, pois com a escrita não vem a expressão corporal, não vem a emoção, não vem a entonação, não vem a visualização do objeto como na linguagem oral, portanto é de suma importância que se caracterize o objeto em questão colocando a unidade específica dele, pois é esta que dá a natureza do que estamos trabalhando. Se você responde somente 35, por exemplo, esse 35 se refere a quê? Idade, balas, metros, metros quadrados, bexigas, dias? Claro que lendo o problema ou a questão saberíamos do que se trata, mas a resposta por si só deve bastar.
Acredito que a importância da resposta completa deve ser passada para o aluno sempre, pois envolve também a sua maneira de se colocar, a sua comunicação oral vai ficando mais objetiva e clara, podendo ele assim exercer com mais facilidade a sua cidadania, não é isto que buscamos!?
O “Cifrão”
O “cifrão” é o sinal que expressa a unidade monetária em nosso país e em muitos outros, ele é representado por “S” cortado com uma ou duas barras.
No caso do Brasil, atualmente o cifrão possui somente uma barra, assim “$”. Nosso país já utilizou em outras épocas o cifrão com duas barras, mas desde que adotamos o “Real” como moeda, usamos o cifrão somente com uma barra.
Claro que isto é um detalhe, mas para mim, um detalhe importante. Não consigo admitir que um brasileiro não consiga representar corretamente sua moeda.
Muitos dos professores participantes colocaram em uma de suas respostas o cifrão com dois traços. Na própria questão comentei que este erro é comum, pelo fato do Brasil já ter adotado o cifrão com dois traços, mas o fato de ser comum não implica que não tenha que ser trabalhado, para tanto, sugiro que observem várias cédulas de reais e possibilitem aos alunos essa observação. Outra sugestão, agora para fixar com os alunos a maneira correta de se representar quantias, é criar modelos de “cheques” e deixar que os alunos preencham, assim estará sendo trabalhado também a escrita (por extenso) da quantia, é uma maneira mais interessante de se trabalhar o velho e conhecido “leia e escreva”. A “Atenção”
Na verdade, foi a “falta de atenção”, a causa de erros de muitos dos professores participantes, que me levou a colocar este item no trabalho.
Nós, professores, sempre cobramos a “atenção” do aluno e comumente dizemos que eles não prestam atenção em nada, mas e nós, prestamos atenção em tudo que fazemos?
A “atenção” é uma coisa de deve ser trabalhada em todos sempre, pois hoje em dia estamos com a vida muito agitada, cheia de problemas, de ruídos, de coisas que tiram nossa atenção, ou a dispersam. Com a criança acontece a mesma coisa e, pode ser ainda pior pelo fato de algumas delas não terem sequer aprendido a ter atenção.
Para trabalhar a “atenção”, penso que a melhor maneira é através de jogos como “jogo da memória”, xadrez, dama, dominó e bingo. Todos estes podem facilmente ser trabalhados na escola. O jogo “paciência” também trabalha bastante a atenção, mas para este já é melhor que se tenha um microcomputador. Aliás, o microcomputador também é ótimo para se trabalhar a atenção, pois ele é por si só interessante para todas as crianças e para a maioria dos adultos.
Considerações Finais
Para desenvolvermos nossa prática, nós, professores, precisamos também desenvolver-nos como profissionais e como sujeitos críticos na realidade em que estamos, isto é, precisamos poder situar-nos como educadores e como cidadãos, pois participamos do processo de construção da cidadania, do reconhecimento de nossos direitos e deveres e da valorização profissional.
A formação da maioria de nós, educadores brasileiros, não contemplou essa dimensão. Não nos foi “ensinado” a ser cidadãos, penso que fomos “programados” para “reproduzir”, então, temos um desafio em nossas mãos: “ensinar” nossos alunos a exercerem sua cidadania, tendo nós mesmos que aprender a exercê-la.
Observando os alunos, os jovens em geral e até muitos adultos, percebi que muitos valores como fibra, justiça, amor à pátria e solidariedade estão se perdendo e, em lugar destes, estão a indiferença, a omissão, a alienação e a discriminação. Penso que temos de resgatar valores nos quais acreditamos, mostrar a realidade aos nossos alunos, mas também fazer com que eles entendam que esta realidade pode ser mudada, que depende de todos nós, de cada um de nós. Temos força, mas usamos mal nossos direitos, escolhemos mal nossos representantes, usufruímos de maneira destrutiva de nossos recursos, nos fechamos em nosso “mundinho” como se nada pudéssemos fazer, ou pior, como se não tivéssemos nada a ver com o que acontece a nossa volta. Um professor não passa somente os conteúdos aos seus alunos, ele é aquele no qual muitos se espelharão.
Hoje, podemos dizer que vivemos no “mundo”, pois os meios de comunicação e a tecnologia encurtaram as distâncias. É muito comum em nossas escolas, alunos que estão separados de seus pais por estes estarem trabalhando em um outro país. Em segundos podemos nos comunicar com alguém de muito longe como se esta pessoa estivesse pertinho de nós. Pela internet temos acesso a museus, bibliotecas e muitas outras coisas. Nosso aluno vive com essa realidade e muitos professores ainda não se deram conta de que precisam se integrar a esse mundo. Já ouvi colegas dizendo que detestam esse tal de computador e nem querem saber de aprender a mexer nele, mas no meu modo de ver, a partir do momento em que uma pessoa escolhe ser “professor” ela passa a ter muitas obrigações e dentre estas a de se atualizar sempre. Como mencionei na “Introdução”, não precisamos “parar” para sermos ultrapassados, basta que diminuamos um pouco nosso ritmo.
Dentre muitas coisas que me chamaram atenção na execução deste trabalho, destaco o receio demonstrado por quase todos os professores participantes em resolver a prova. Eles me perguntavam se a prova seria difícil, diziam que não davam aula na quarta série e por isso não sabiam se iriam bem, enfim, demonstraram muita insegurança para resolver a prova.
Analisando esta reação, percebi que o medo de ser avaliado é comum a professores e alunos. Vem, então, a questão : “Por que sentimo-nos assim diante da ‘avaliação’?”
Não vou dizer a você que foi fácil realizar este trabalho, na verdade, foi mais um desafio, pois eu não tinha a mínima idéia do que fosse uma monografia. Um trabalho como este exige muita leitura e dedicação, mas você começa a escrever, vai se “apaixonando” pelo que está fazendo e, quando chega ao final, sente uma sensação maravilhosa, como a que eu estou sentindo agora, é satisfação, é alegria, é orgulho de si mesma... Você já fez um trabalho deste tipo? Então faça, garanto que você não irá se arrepender!
Referências Bibliográficas
BRASIL – Secretaria de Educação Fundamental. Parâmetros Curriculares Nacionais: Matemática – Ensino de 1ª. à 4ª. Série. Brasília: MEC/SEF, 1997.
BRASIL – Secretaria de Educação Fundamental. Parâmetros Curriculares Nacionais: Temas Transversais – Ensino de 1ª. à 4ª. Série. Brasília: MEC/SEF, 1997.
DAVIS. C; ESPÓSITO, Y. L. Papel e Função do Erro na Avaliação Escolar. Cadernos de Pesquisa, São Paulo, n. 74, p. 71-75, agosto 1990.
Enciclopédia Brasileira Mérito; Volume 13; Editora Mérito S.A., p. 205-206.
KOCH, Nancy Terezinha Oldenburg. Um Teste de Rendimento de Matemática. Londrina, 1997. Monografia – Universidade Estadual de Londrina.
LONDRINA. Secretaria Municipal de Educação. Proposta Curricular de Pré-Escola e 1ª à 4ª Série do 1º Grau da Rede Municipal de Londrina, 1992.
MORI, Iracema; ONAGA, Dulce Satiko. Matemática – Idéias e Desafios – 5ª Série; 5ª Edição, Editora Saraiva, São Paulo, 1998.
MULLER, Mary Stela; CORNELSEN, Julce Mary. Normas e Padrões para Teses, Dissertações e Monografias. 2ª Edição. Editora UEL. Londrina, 1999.
SÃO PAULO – Secretaria de Estado da Educação. Atividades Matemáticas 4ª. Série do 1º. Grau. 2ª. Edição, São Paulo: SE/CENP, 1994.
SOUZA, Clarilza Prado de. Avaliação do Rendimento Escolar. Editora Papiros, 1993.
ANEXOS
ANEXO A
ANEXO B
[1] Como quero que este trabalho seja como uma “conversa” entre mim e o leitor, toda vez que me referir à “você”, é ao leitor do momento a quem me refiro. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| © Copyright 2004 - Powered by Algacir Soriani - algacir.soriani@sercomtel.com.br - 9/3/2026 21:4 - acessos: 64744 |

|